Simon Says

Aspiring Polymath

About me
Contact

Almost Orthogonal Vectors

First published: 24th April 2025

Last updated: 30th April 2025

I came across this claim in a machine learning paper

As a result, an n-dimensional representation may encode features not with the n basis directions (neurons) but with the \propto \exp(n) possible almost orthogonal directions (Elhage et al., 2022b) , leading to polysemanticity.

All that the reference had to say about it was this:

Although it's only possible to have n orthogonal vectors in an n-dimensional space, it's possible to have \exp (n ) many "almost orthogonal" ( \lt \epsilon cosine similarity) vectors in high-dimensional spaces. See the Johnson—Lindenstrauss lemma .

For us mere mortals, let's fill in some of the gaps here.

Almost Orthogonal

What does it mean to be "almost orthogonal" anyway? Two vectors are orthogonal if the angle between them is a right angle, or equivalently, if their dot-product is 0 .

The angle \theta between two vectors u, v \in \mathbb{R}^n is given by u \cdot v = \|u\| \|v\| \cos \theta , or \cos \theta = \frac{(u \cdot v)}{\|u\| \|v\|}

Thus we can pick a small \epsilon and say that two vectors are almost orthogonal if |\cos \theta | \lt \epsilon

Proof using the Johnson—Lindenstrauss Lemma

The lemma states:

Given 0 \lt \epsilon \lt 1 , a set X of N points in \mathbb {R}^n , and an integer k \gt 8(\ln N) / \epsilon ^ 2 , there is a linear map f : \mathbb {R}^n \rightarrow \mathbb {R}^k such that (1-\varepsilon )\|u-v\|^2\leq \|f(u)-f(v)\|^2\leq (1+\varepsilon )\|u-v\|^2 for all u, v \in X .

To translate this into an expression about angles, note that

\|u-v\|^2 = \|u\|^2 + \|v\| ^2 - 2 u \cdot v = \|u\|^2 + \|v\| ^2 - 2 \|u\| \|v\| \cos \theta

We can rearrange this to get an expression for \cos \theta

\cos \theta = \frac{\|u\|^2 + \|v\|^2 - \|u-v\|^2}{2 \|u\| \|v\|}

As the transformation f is linear, f(0) = 0 , so putting u = 0 , we get

(1-\varepsilon )\|v\|^2\leq \|f(v)\|^2\leq (1+\varepsilon )\|v\|^2

Now, let \theta ^{\prime} be the angle between f(u) and f(v)

\cos \theta ^{\prime} = \frac{\|f(u)\|^2 + \|f(v)\|^2 - \|f(u)-f(v)\|^2}{2 \|f(u)\| \|f(v)\|}

We can now compare the angles

\frac{(1-\epsilon)}{(1 + \epsilon)} \cos \theta \leq \cos \theta ^{\prime} \leq \frac{(1+\epsilon)}{(1 - \epsilon)} \cos \theta

So if we take our n points to be exactly orthogonal vectors in \mathbb{R}^n , they will be mapped to almost-orthogonal vectors in \mathbb{R}^k .

Since the lemma holds for k \gt 8(\ln N) / \epsilon ^ 2 , we can fix \epsilon and have N grow exponentially with k . QED.

Thinking Geometrically

I found the above argument persuasive but not very intuitive. Here is a scheme I came up with for getting a better feeling of why this happens in high dimensions even though it isn't the case in 2 or 3 dimensions.

We are going to pick points on the unit sphere one by one. Points on the sphere obviously correspond to unit vectors. After picking a point p , we will shade out on the sphere all points q that are "not orthogonal enough" to p (i.e. \cos \theta is too large).

Figure 1: After we have picked our first point (shown here at the north pole), we shade out the areas (grey) that are too close to p and -p

At each step, we will only be allowed to pick a point if it isn't shaded in. As we add more and more points to our set, more and more of the area of the sphere will be shaded in, until eventually we run out of space.

Figure 2: After adding each point, we shade out more of the sphere.

As a very rough lower bound, we know that the number of points we can pick before this happens is at least the total surface area of the sphere divided by the area that each point will cause to be shaded. In practice, this is a huge underestimate because there will be a lot of overlap in the shaded regions.

The area of a strip on an (n-1)-sphere between \theta and \theta + \mathrm{d} \theta , is the area of an (n-2)-sphere with radius \sin \theta , multiplied by \mathrm{d} \theta .

The area of a (n-2)-sphere with radius r is some constant times r^{n-2} .

Thus the proportion of the sphere that is not shaded grey after we have added the first points is

\frac{\int_{\pi/2-\epsilon}^{\pi/2+\epsilon} \sin^{n-2} \theta \mathrm{d} \theta}{\int_0^{\pi} \sin^{n-2} \theta \mathrm{d} \theta}

Now, as n gets big, \sin^n \theta gets very very sharply peaked around \theta = \pi/2 , so most of the area is concentrated in that central white band.

Here is a plot of \sin^n \theta for n=20 :

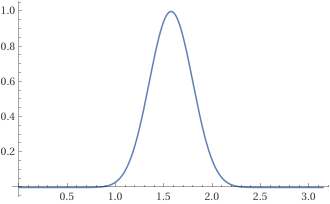
And here is n=700 :

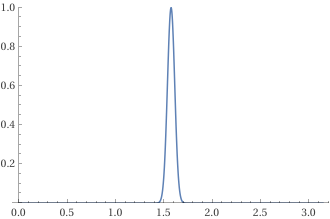
The proportion of the grey area is:

\frac{g}{g+w} = \frac{\int_0^{\pi/2-\epsilon} \sin^{n-2} \theta \mathrm{d} \theta}{\int_0^{\pi/2} \sin^{n-2} \theta \mathrm{d} \theta} = \frac{\int_0^{\pi/2-\epsilon} \sin^{n-2} \theta \mathrm{d} \theta}{\int_0^{\pi/2-\epsilon} \sin^{n-2} \theta \mathrm{d} \theta + \int_{\pi/2-\epsilon}^{\pi/2} \sin^{n-2} \theta \mathrm{d} \theta}

In the range 0 \leq \theta \leq \pi/2 - \epsilon , we use \sin \theta \leq \theta .

This tells us that

g \lt \int_0^{\pi/2-\epsilon} \theta^{n-2} \mathrm{d} \theta = \left[\frac{1}{n-1} x^{n-1} \right]_0^{\pi/2-\epsilon} = \frac{1}{\pi/2 - \epsilon}^{n-1}

In the range \pi/2 - \epsilon \leq \theta \leq \pi/2 , we let x = \pi/2 - \theta and use \sin (\theta) = \sin (\pi/2 - x) = \cos x \geq e^{- x^2} (see graph).

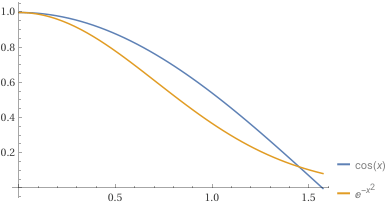
This tells us that

w = \int_{\pi/2-\epsilon}^{\pi/2} \sin \theta ^{n-2} \mathrm{d} \theta = \int_0^{\epsilon} \cos x ^{n-2} \mathrm{d} x \gt \int_0^{\epsilon} e ^{-(n-2)x^2} \mathrm{d} x = \frac{1}{2} \sqrt{\frac{\pi}{n-2}} \mathrm{erf} (\sqrt {n-2} \epsilon)

Where \mathrm{erf} is the integral of the Gaussian normal. As n \rightarrow \infty , this tends to 1.

As g shrinks exponentially in n but w behaves like 1 / \sqrt n for large n , the fraction of the sphere that is shaded grey at each step shrinks exponentially in n .

So there you have it. For fixed \epsilon , the number of vectors we can find where every pair has an angle within \epsilon of a right angle is exponential in n . This is because the area of the sphere is being concentrated around the equator.

Copyright 2025

RSS Feed