Snyk Fetch The Flag 2025 - D0nutShop (Medium)
First published: 4th March 2025
Last updated: 6th March 2025
This post is one of a series of write-ups from a competition called Fetch The Flag. You can read more about the competition and see write-ups of other challenges here .
Disclaimer: I did this challenge after the live competition was over.
The prompt for this challenge was:
The donuts at D0nutShop are so good, you'll hit the Math.floor()!
The site looks like this when you load it up:
We are given login credentials for a user called d0nut, and there is also a user called admin but we don't have the password for that account. The application also includes an API for resetting passwords. The API has these endpoints:
- /reset - generates an OTP code for the provided username
- /reset/api/get-otp - returns the OTP code for the provided username if you also send the correct password
- /reset/verify - checks if an OTP code is valid and stores the result in your session
- /reset/change-password - let's you set a new password if you have the correct session state from above
Looking through the code, my first thought was prototype pollution:

I could tell them my username was __proto__...
But the prompt and the landing page are pointing us somewhere else:
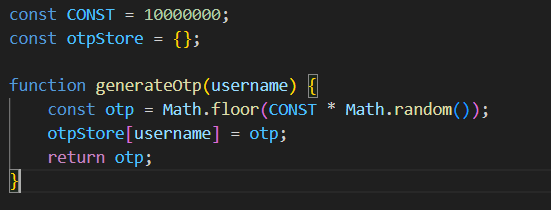
I knew that Math.random was not a secure random number generator. But there is a difference between knowing something is insecure and being able to exploit it. I found this script online that recovers the internal state of Math.random based on observing a few outputs but it expects to know the full output, whereas we only have the first 7 decimal digits.
The modern Math.random is based on XorShift128+. We don't need to know too much detail about this algorithm. It has 64 bits of internal state. Every time Math.random is called, some of those bits are returned, and the internal state is updated deterministically. When we ask for a float, we get 52 of those bits and the other 12 remain unknown.
The script I found takes the known bits, and applies those as Boolean constraints on the initial internal state. Then it throws all of these equations into a SAT solver. Lovely.
When we call Math.floor(CONST * Math.random()), we keep the first 7 decimal digits of this float, which corresponds to 23 bits. So we lose 52-23=29 bits in this process.
After a bit of trial and error, I made the following change to the script:

This throws away 32 of the 52 bits in the Mantissa. We could get away with throwing out only 29 bits, but I only did these bit calculations while writing this, after the challenge was over. Anyway, if we throw away too much information, the only downside is that we will need to collect a few more OTP codes before we know enough to recover the full internal state of Math.random.
Then, as d0nut, we request OTP codes and feed them into the program until it starts predicting correctly.
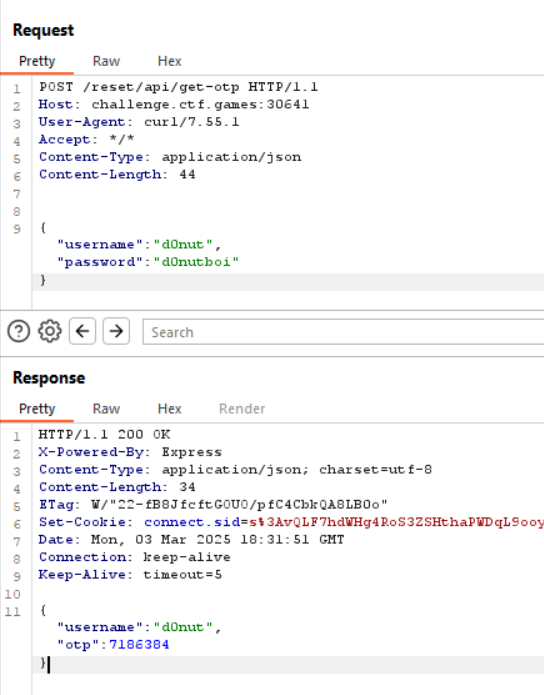
Now it's time to request an OTP code for admin:

We don't get to view this one with the API, but we know what it is because we have a python script that has reverse-engineered the internal state of Math.random.
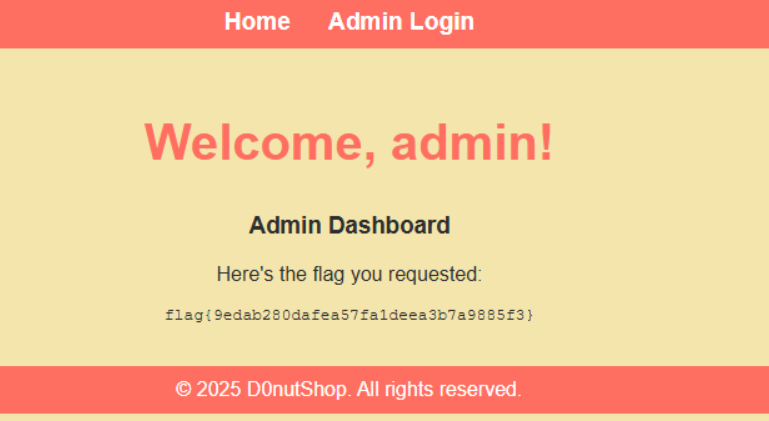
After verifying the OTP, we get to set a new password for the admin account.
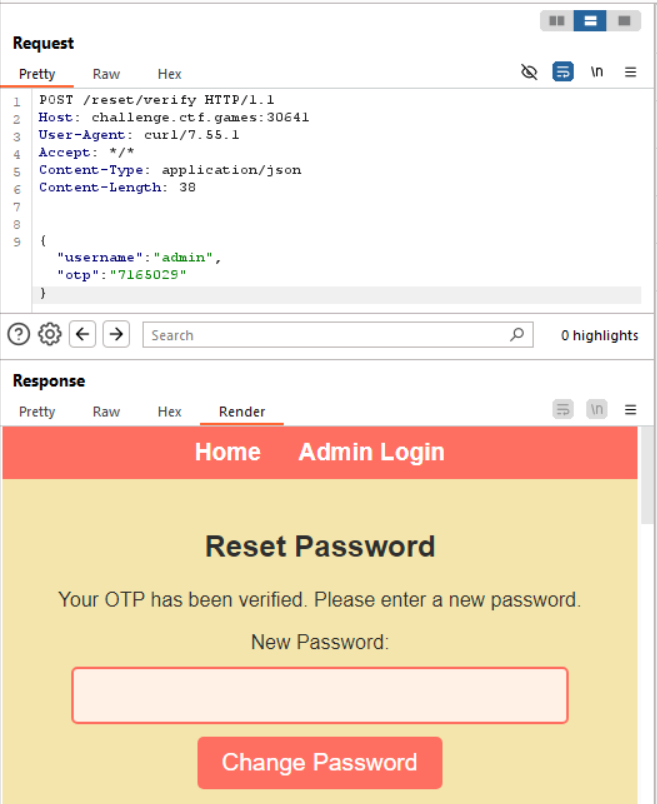
Then we can log in and retrieve the flag! Hooray!
_ Likes